Considerations of Fluid Flow in Syringe Pump Operations

You have a liquid and need to select an appropriate syringe pump and tubing for your application. However, you are unsure which pump will work, what tubing to use, and whether the flow rate will affect the performance of the pump.

These and related questions often surface among those looking to configure a pumping setup for their needs. It is essential to consider the viscosity of your fluid and the physical aspects of flow to maximize pumping performance, minimize shear stress, and address other potential issues. Here are a few considerations to help establish the appropriate setup.

Physical principles of flow

Viscosity

Firstly, viscosity is a property that determines how liquids flow under certain conditions¹. This property can be summarized as a liquid’s internal resistance to flow at a given rate or the relative “thickness” of that liquid². The SI unit of viscosity is Pascal-second (Pa·s). Viscosity is more commonly expressed in centipoise (cP), a convenient measure based on 1 cP being equal to the viscosity of water at 20 °C. Ten cP is equal one Pa·s (10 cP = 1 Pa·s).

Fluid forced through a tube will exhibit faster flow near the center and slower flow at the fluid layers that touch the tube’s inner surface. For a liquid to flow through the tube, the force exerted pushing the fluid (the action of the syringe pump) must overpower the internal friction within the fluid, which is caused by viscosity. Viscosity depends on a fluid’s state, which is impacted by temperature and pressure. By heating a liquid, the frictional forces within the liquid and at the liquid-tube interface are lowered, and in effect, so is the viscosity. This means less force is required to push the liquid through the tube and, by relation, a set pressure can result in an elevated flow rate.

The takeaways here are that you can pump lower−viscosity liquids more easily under lower pressure and temperature, while higher−viscosity liquids require a higher pressure and temperature to achieve a similar flow rate.

Shear stress

Another important consideration involves the property of shear. The force applied to push the liquid through the tubing (the pumping pressure) must be controlled to be sure that shear stress does not damage the liquid and its particle components³.

As a fluid moves along a solid boundary, such as the inner face of the tubing, it is subjected to shear stress. Shear stress arises from shear force and is defined as tau (average shear stress) equal to force per unit area. As the applied force is increased, so is the shear stress. As the area is increased (diameter of tubing), the shear stress can be affected as well.

High shear stress can damage the integrity of liquids and the behavior of solutes and dissolved particles. Excess shear stress when pumping liquids such as salt solutions can result in precipitation. Pumping complex liquids, such as fracking solutions, can result in mixed, unpredictable solutions if not properly controlled for shear stress. For these reasons, it is important to select the right type of pump, the proper diameter and type of tubing, as well as the correct pump flow rate that is best fit for the liquid and the application.

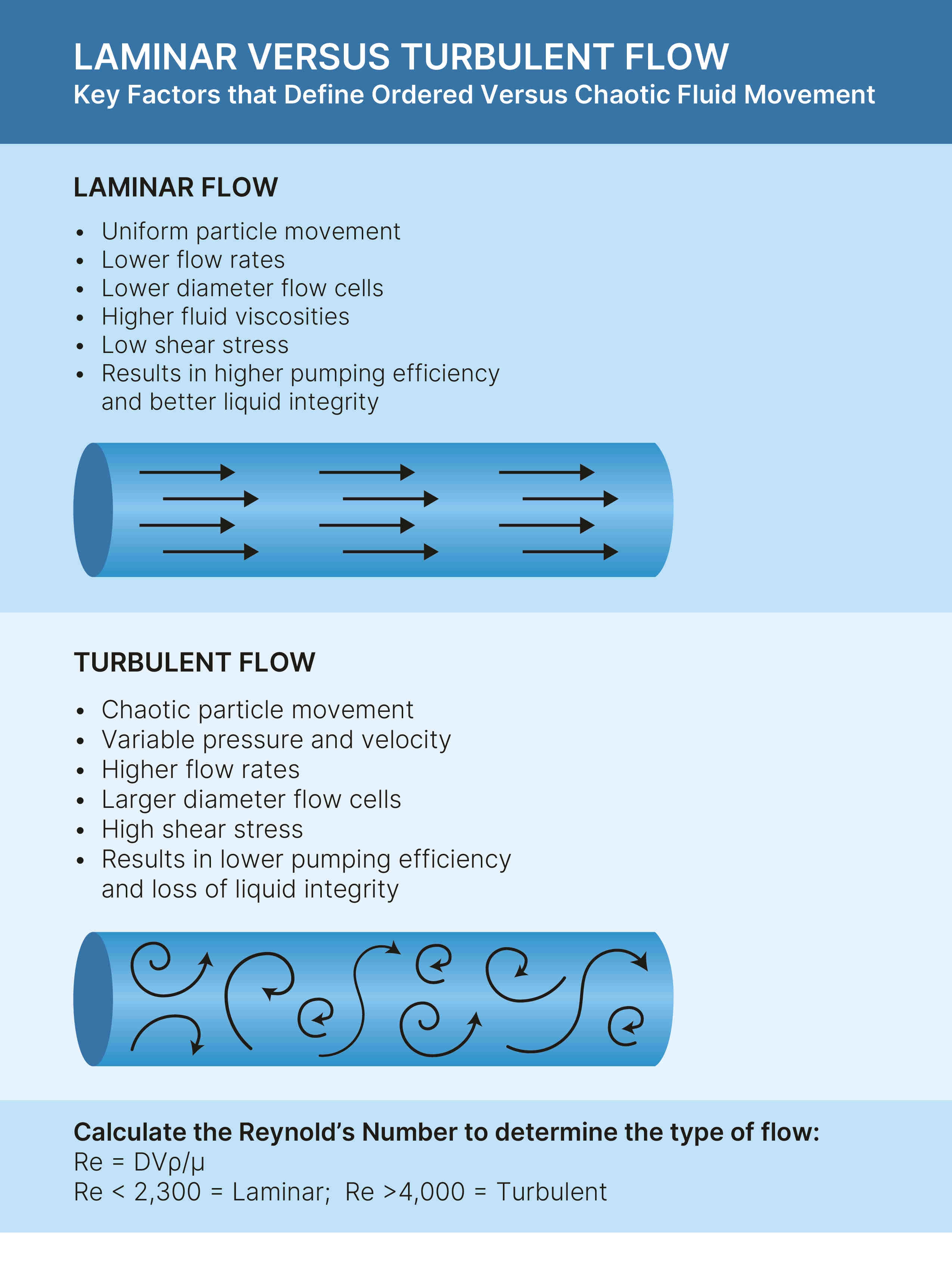
Laminar versus turbulent flow

Laminar flow is defined as the movement of a liquid where every particle follows the same path. This orderly and predictable flow is directly related to the applied pressure. Laminar flow is more likely to result from lower flow rates and higher viscosity liquids. Laminar flow is also associated with low sheer stress applied to the liquid and is, therefore, conducive to maintaining fluid integrity.

Turbulent flow is chaotic and is associated with constant variations in pressure and velocity through the flow channel. Due to the dynamic and random movement of particles and the variability of physical influences, turbulent flow is associated with high sheer stress applied to the liquid.

In order to keep physical properties intact, a liquid flowing through a flow cell or tubing must be maintained under laminar flow conditions.

How to calculate the flow rate and tubing diameter needed for your application

To identify laminar flow conditions and to minimize the risk of shear stress, it is helpful to have a few equations to solve for infusing a liquid^4,5,6,7.

The first step is to identify the volume of liquid you intend to pump and the desired pump rate. This equation will provide details on the tubing diameter to begin with.

V = Q/A

V = Velocity of fluid pumping in m/sec

Q = Flow rate - volume/time (m³/sec)

A = Cross-sectional area of tubing (π r²); where: r = diameter (D)/2

* Cross-sectional area of the tubing is proportional to the square of the diameter of the tubing

Next, it is important to consider the viscosity of the liquid and its behavior according to your pumping rate and tubing diameter. Solving for the Reynold’s Number of the liquid will help determine whether the fluid flow will induce excess shear stress on the liquid, i.e. Laminar versus Turbulent flow conditions.

Reynold’s Number:

R_e = DVρ/µ

D = Diameter of tubing (m)

V = Fluid velocity (m/sec)

ρ = Density of the fluid – mass per volume (kg/m³)

µ = Absolute viscosity (cP or 0.1 Pa·s)

Absolute viscosity:

µ = νρ

ρ = Density of the fluid (kg/m³)

ν = Kinematic viscosity (m²/sec or Stoke (St))

*Kinematic viscosity is empirically determined using a glass capillary viscometer.

*Kinematic viscosity of common liquids can be found here.

In a fully developed flow, laminar flow occurs when the Reynold’s Number (R_e) is <2,000 and turbulent flow occurs when R_e is >4,000⁷. A mixed state called transition flow occurs between 2,000 and 4,000 R_e. Since turbulent flow (and transition flow to a lesser extent) can involve significant shear stress, a Reynold’s Number (R_e) that falls within – and not exceeding - the range of laminar flow is preferable.

Summary

Your application should consider both the pumping rate and the diameter and type of tubing for your liquid. These key parameters are best identified by calculating the Reynold’s Number for your liquid and ensuring that shear stress is minimized by maintaining laminar flow in the pump program setup. To achieve an acceptable Reynold’s Number while protecting the integrity of your liquid, you should adjust the flow velocity (pumping rate) and/or the flow channel or tubing dimensions (diameter) as needed.

Lowering the viscosity of your liquid through heating or dilution allows for a lowered pumping pressure to achieve the same flow rate. Pressure and temperature capabilities are additional pump features that should also be taken into consideration when selecting the best syringe pump for your application.

In the end, a balance must be struck between all these parameters in order to achieve the requirements of laminar flow and maintain the integrity of your liquid.

Published in partnership with Chemyx.

References:

1.      https://www.byk-instruments.com/en/t/knowledge/viscometry-measurement

2.      https://physics.info/viscosity/

3.      https://autmix.com/en/blog/how-stress-shear-works-in-fluids

4.      https://www.sugarprocesstech.com/pump-related-formulas/

5.      https://courses.lumenlearning.com/suny-physics/chapter/12-1-flow-rate-and-its-relation-to-velocity/

6.      https://www.engineeringtoolbox.com/kinematic-viscosity-d_397.html

7.      https://www.sciencedirect.com/topics/engineering/reynolds-number